Learning effects lead to path dependency

First Posted: 2021.05.22, Last Revised: 2021.05.22, Author: Tom Brown

Learning effects lead to path dependency
Including learning in your model => many distinct local optima
=> Diverse choice of low-cost future energy systems
Can't just look at one

Conclusions from Niclas Mattsson's pioneering work in 1990s:

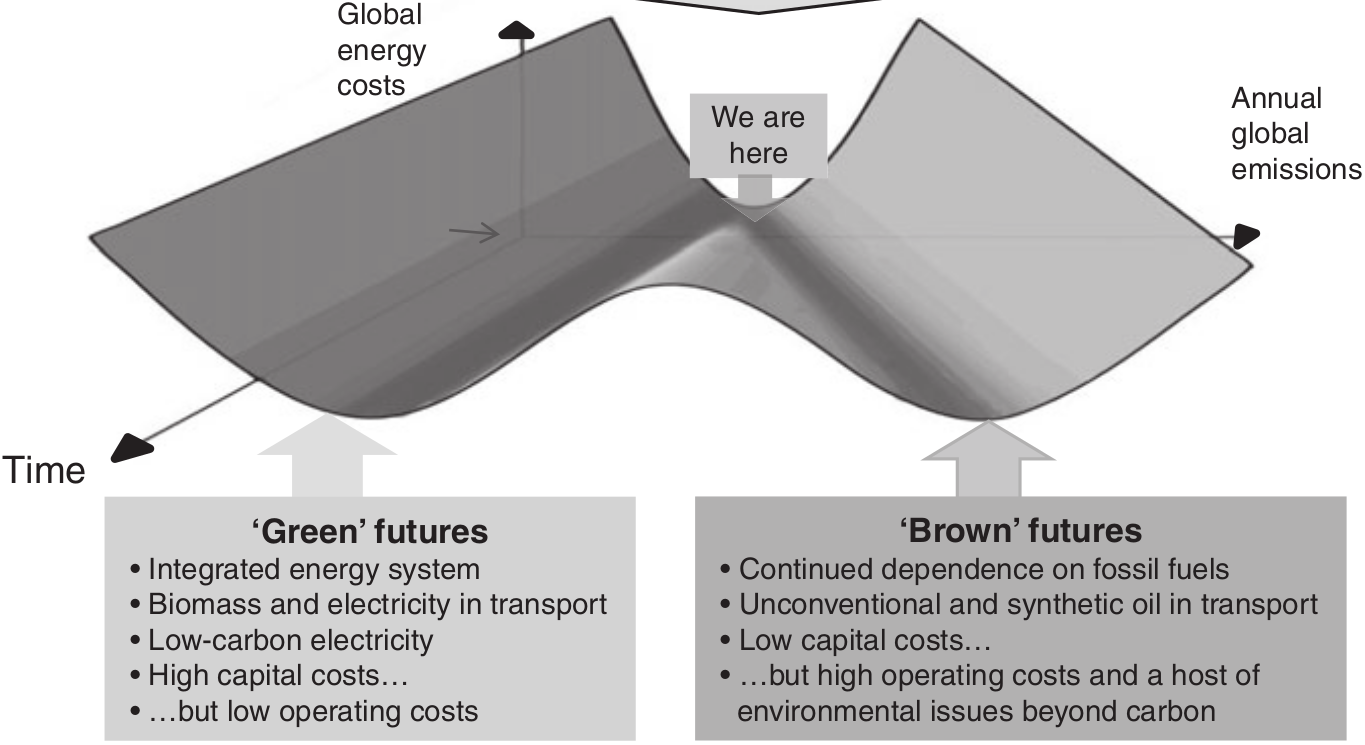
Figure 1: (Source: fabulous book Planetary Economics by Michael Grubb)

So what did Niclas do?

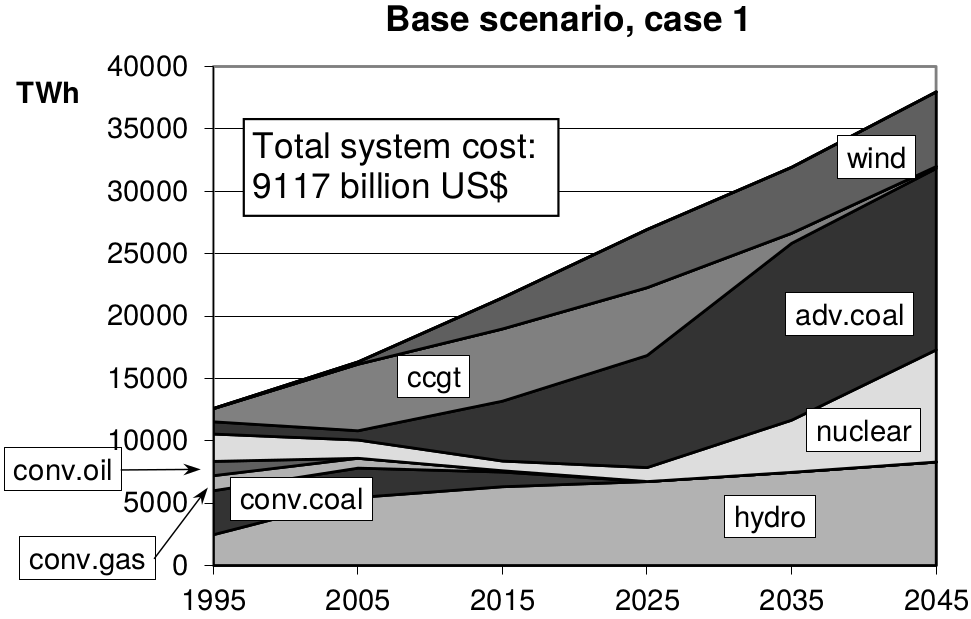
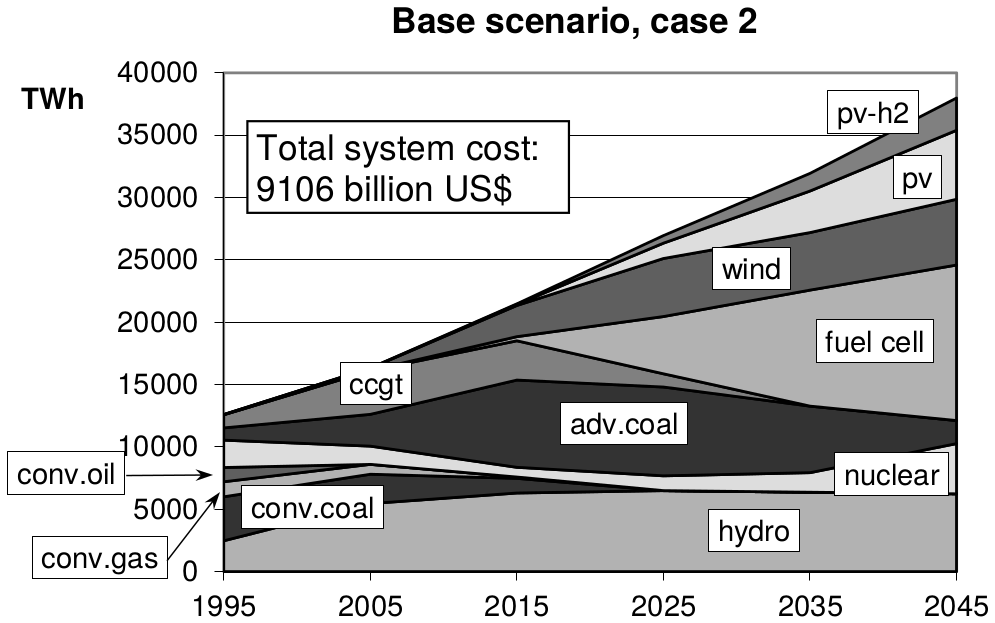
He ran an energy model with built-in learning curves and showed that with exactly the same model (same equations, all same data inputs, costs, etc.) you can get radically different energy pathways with similar total costs:

Case 1 is coal-heavy while Case 2 has lots of PV. They cost roughly the same.

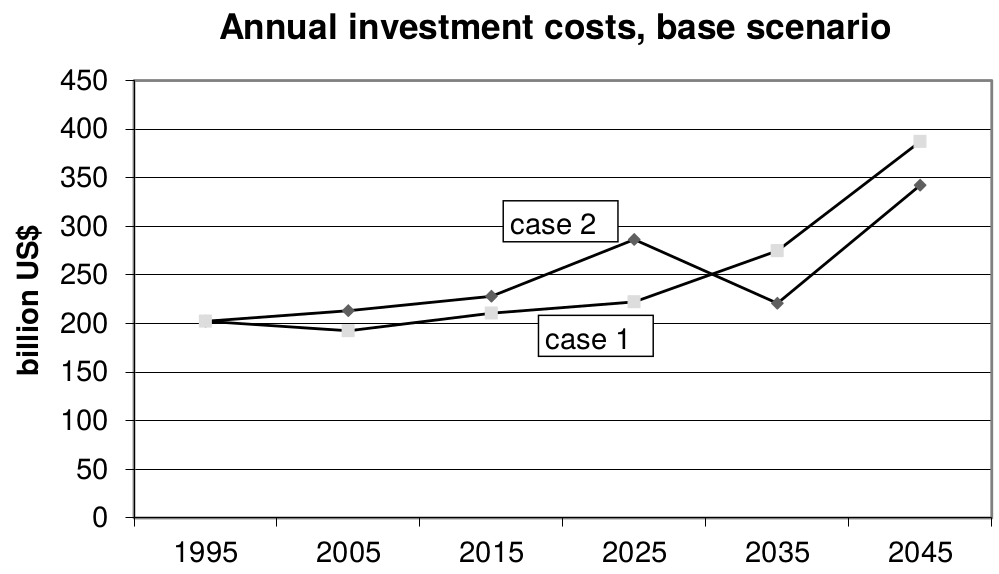
Case 2 is different because large investments get triggered early for PV and other technologies, which take them down the learning curve, saving costs later in the simulation:

This phenomenon, that technology investments and learning now can save costs later, was well understood by the fathers of the German renewable subsidies programmes, Hermann Scheer and Hans-Josef Fell, which brought down the costs of PV.

How can the same model deliver such different results?

Because learning curves introduce non-convexities into the optimisation.

This leads to local optima in the solution space.

Depending on where the solver starts looking (green/blue), you end up in different optima:

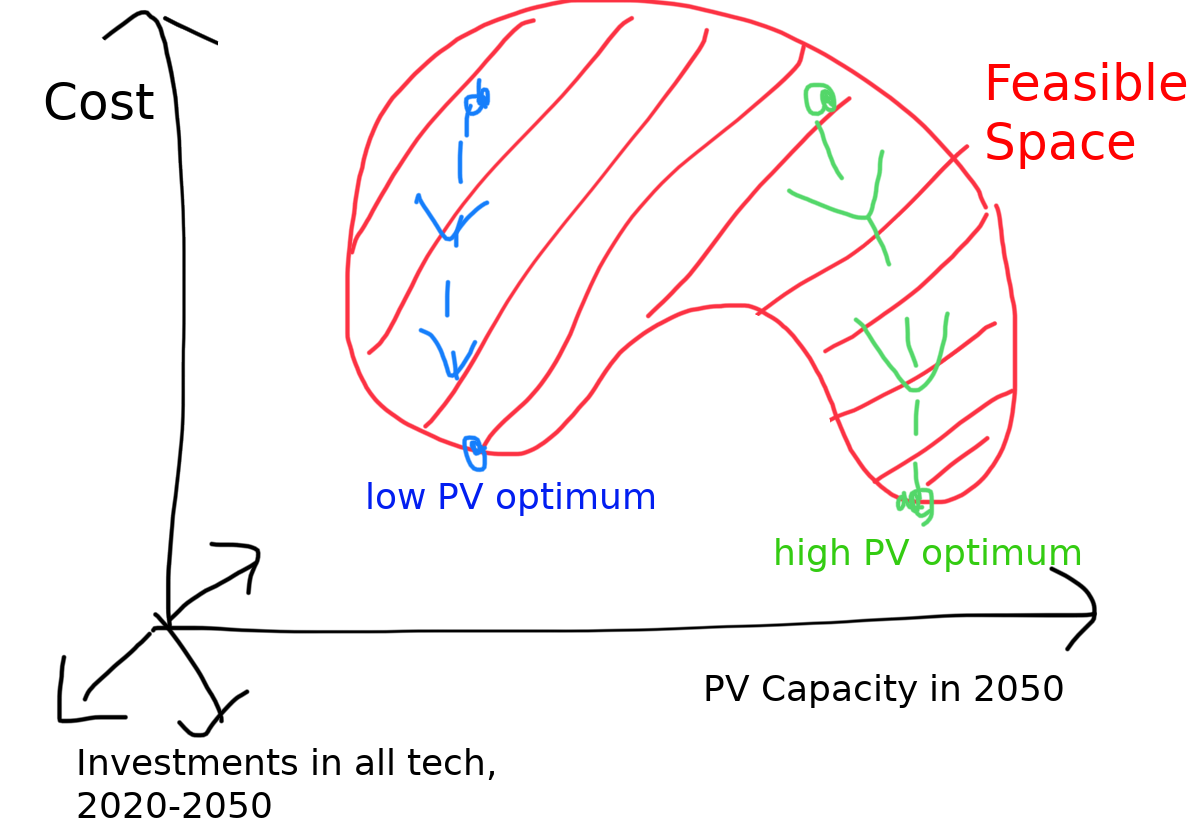
If the solver starts its search on the left and looks for decreasing cost, it lands at the blue low-PV, high-coal optimum.

If it starts on the right, it lands in the green high-PV optimum.

It's hard to build solvers to find these different solutions, so they're often ignored.

This diversity often goes unacknowledged in the energy modelling world where models that have endogenous learning curves aren't used to explore all solutions. (Please correct me if I'm wrong.)

Policy-wise, this general phenomenon of path dependency shows how we can choose (within limits) how we steer our technology investment towards solutions that society wants (e.g. high acceptance, high co-benefits, etc.).

Conclusion: there are lots of different possible low-cost low-emission energy systems out there, depending on which technologies we choose to invest in.

Now for some more technical details.

This is NOT the same as the near-optimal solutions that crop up in the Method to Generate Alternatives, since those solutions are convexly connected to the global optimum. Here we're talking about far-away distinct near-optimal solutions.

Niclas has some comments on this:

What about models that approximate the non-linear learning curves with a piecewise linearisation to turn it into a MILP? (A technique Niclas co-invented with Sabine Messner)

Niclas has a trick to find the local optima by forcing constraints and seeing if they become non-binding: